Innehåll

• Steg
• tips

Matematiker och grafikprogrammerare behöver ofta hitta vinkeln mellan två vektorer. Lyckligtvis kräver formeln som används för att beräkna denna vinkel inte mer än en enkel skalprodukt. Även om resonemanget bakom denna formel är lättare att förstå när vi använder tvådimensionella vektorer, kan vi enkelt anpassa den till vektorer med valfritt antal komponenter.

Steg

Del 1 av 2: Beräkna vinkeln mellan två vektorer

1. 

   Identifiera de två vektorerna. Skriv ner all känd information om de två vektorerna. I syftet med denna självstudie kommer vi att anta att du känner till vektorerna endast när det gäller deras dimensionella koordinater (kallas också komponenter). Om du redan känner till modul eller standard av dessa vektorer (det vill säga deras längd) kan du hoppa över några av stegen nedan.
   • Exempel: vi tar hänsyn till de tvådimensionella vektorerna = (2,2) och = (0,3). Dessa två vektorer kan skrivas om som = 2jag + 2j e = 0jag + 3j = 3j.
   • Även om vårt exempel använder två tvådimensionella vektorer kan vi tillämpa följande instruktioner på vektorer med valfritt antal komponenter.

2. 

   
   
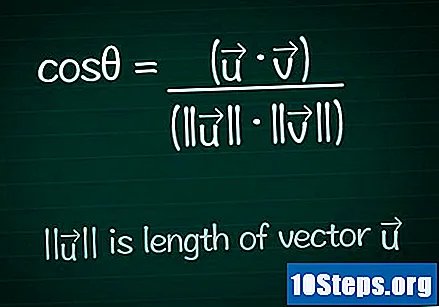
   Skriv kosinusformeln. För att hitta värdet på vinkeln θ mellan två vektorer måste vi först beräkna kosinus för den vinkeln. Du kan söka och ta reda på formeln i detalj eller helt enkelt skriva den som nedan:
   • cosθ = (•) / (|||| ||||)
   • |||| representerar modul (eller längd) på vektorn ".
   • • representerar skalprodukt (eller intern produkt) av de två vektorerna.

3. 

   
   
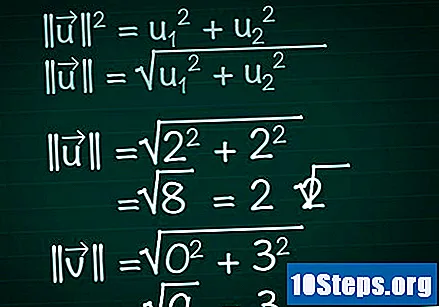
   Beräkna modulen för varje vektor. Föreställ dig en rätt triangel som bildas av komponenten x av en vektor, dess komponent y och själva vektorn. I denna triangel spelar vektorn hypotenusen; därför, för att hitta dess längd, kommer vi att tillämpa Pythagorean teorem. Som ett resultat är denna formel lätt tillämpbar på vektorer med valfritt antal komponenter.
   • || u || = u₁ + u₂. Om vektorn har mer än två komponenter, fortsätt bara att lägga till + u₃ + u₄ +...
   • Därför måste vi för en tvådimensionell vektor || u || = √ (u₁ + u₂).
   • I vårt exempel är |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
   Beräkna skalprodukten mellan de två vektorerna. Du bör redan känna till metoden för att multiplicera vektorer, även kallad skalprodukt. För att beräkna skalprodukten av två vektorer i termer av deras komponenter multiplicerar vi komponenterna i samma riktning med varandra och lägger sedan till resultaten av dessa produkter.
   • Om du arbetar med datorgrafikprogram, besök först avsnittet "Tips" innan du fortsätter.
   • I matematiska termer, • = u₁v₁ + u₂v₂, där u = (u₁, u₂). Om din vektor har mer än två komponenter, fortsätt bara att lägga till + u₃v₃ + u₄v₄...
   • I vårt exempel • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. Detta är värdet på skalprodukten mellan vektorerna och.

5. 

   Ersätt dessa resultat i kosinusformeln. Kom ihåg att cosθ = (•) / (|||| || ||). Vi har redan beräknat skalprodukten och modulen för de två vektorerna. Låt oss nu ersätta dessa värden i formeln och beräkna kosinusens vinkel.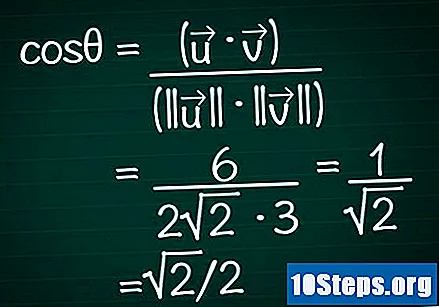
   • I vårt exempel är cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Hitta vinkeln baserad på din kosinus.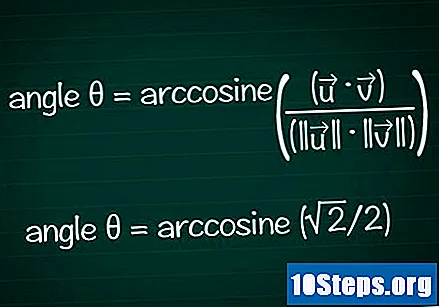
   Använd din räknares båge- eller cos-funktion för att bestämma vinkeln θ från ditt kosinusvärde. I vissa fall kanske du kan hitta vinkelvärdet baserat på enhetscirkeln.
   • I vårt exempel är cosθ = √2 / 2. Skriv "arccos (√2 ​​/ 2)" i din räknare för att hitta vinkeln. Ett annat alternativ är att leta efter vinkeln θ på enhetscirkeln där cosθ = √2 / 2: detta kommer att vara sant för θ = /₄ eller 45 °.
   • När vi samlar all information kommer vi att ha den slutliga formeln θ = arccosine ((•) / (|||| || ||))

Del 2 av 2: Definiera formeln för beräkning av vinkeln

1. 

   Förstå syftet med formeln. Formeln vi använde för att beräkna vinkeln mellan två vektorer härleddes inte från tidigare existerande regler; istället skapades den som en definition av skalprodukten mellan två vektorer och vinkeln mellan dem. Detta beslut är dock inte godtyckligt. Med en närmare titt på grundläggande geometri kan vi se varför denna formel resulterar i så användbara och intuitiva definitioner.
   • Följande exempel använder tvådimensionella vektorer eftersom de är den mest intuitiva typen att arbeta med. Vektorer med tre eller flera dimensioner har sina egenskaper definierade utifrån den allmänna formeln (också på ett mycket liknande sätt).

2. 

   Granska kosinuslagen. Tänk på vinkeln θ som bildas av sidorna i valfri triangel De och B och sidan ç mitt emot den vinkeln. Enligt kosinuslagen är c ​​= a + b -2abmidjeband(Θ). Demonstrationen av denna formel kan lätt erhållas genom kunskap om grundläggande geometri.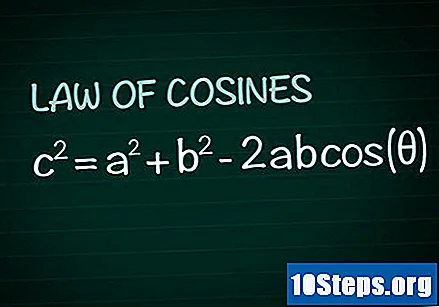

3. 

   Anslut de två vektorerna för att bilda en triangel. Rita ett par vektorer, och med en vinkel θ mellan dem. Rita sedan en tredje vektor mellan dem för att bilda en triangel. Med andra ord, rita vektorn så att + =, eller helt enkelt = -.

4. 

   Tillämpa kosinuslagen på denna triangel. Byt ut längden på sidorna på vår vektor triangel (det vill säga vektormodulen) i formeln för kosinuslagen:
   • || (a - b) || = || a || + || b || - 2 || a || || b ||midjeband(θ)

5. 

   Omskriva formeln med skalprodukter. Kom ihåg att punktprodukten är förstoringen av en vektor som projiceras på en annan. Den skalära produkten av en vektor i sig kräver inte projektion eftersom det inte sker någon riktningsförändring. Detta betyder att • = || a ||. Baserat på denna information, låt oss skriva om ekvationen för kosinuslagen:
   • (-) • (-) = • + • - 2 || a || || b ||midjeband(θ)

6. 

   Förenkla formeln. Expandera produkterna på vänster sida av ekvationen och förenkla den sedan tills du når formeln vi känner för beräkning av vinklar.
   • • - • - • + • = • + • - 2 || a || || b ||midjeband(θ)
   • - • - • = -2 || a || || b ||midjeband(θ)
   • -2 (•) = -2 || a || || b ||midjeband(θ)
   • • = || a || || b ||midjeband(θ)

tips

• För snabb upplösning, använd följande formel på valfritt tvådimensionellt vektorpar: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• Om du arbetar med datorgrafikprogram behöver du sannolikt bara veta riktningen för vektorerna, inte deras längd. Följ stegen nedan för att förenkla ekvationerna och snabba upp ditt program:
  • Normalisera varje vektor, det vill säga hitta enhetsvektorn som har samma riktning som den ursprungliga vektorn. För att göra detta, dela varje komponent i vektorn med vektormodulen.
  • Beräkna skalprodukten för de normaliserade vektorerna, inte de ursprungliga vektorerna.
  • Eftersom modulen (det vill säga längden) för de normaliserade vektorerna är enhetlig kan vi lämna dem utanför formeln. Din slutliga ekvation för att beräkna vinklar är bågar (•).
• Baserat på formeln för kosinuslagen kan vi snabbt ta reda på om vinkeln i fråga är akut eller stöt. Börja med cosθ = (•) / (|||| ||||):
  • Ekvationens vänstra och högra sida måste ha samma tecken (positivt eller negativt).
  • Eftersom längderna alltid är positiva kommer cosθ alltid att ha samma tecken som skalprodukten.
  • Därför, om den skalära produkten är positiv, kommer cosθ att vara positiv. Detta innebär att vinkeln är i den första kvadranten i enhetscirkeln, det vill säga θ <π / 2 eller 90 °. Därför är vinkeln akut.
  • Om den skalära produkten är negativ är cosθ negativ. Detta betyder att vinkeln är i den andra kvadranten i enhetscirkeln, det vill säga π / 2 <θ ≤ π eller 90 ° <θ ≤ 180 °. Därför är vinkeln stöt.